tonglin0325的个人主页

特征预处理——特征选择和特征理解

tonglin0325

1.数据可视化

1.单变量可视化

参考：从kaggle房价预测看探索性数据分析的一般规律

查看pandas某列的统计指标

1
2
3
4
5
6
7
8
9
10
11
12
13
# 描述性统计
print(train_data['SalePrice'].describe())

count      1460.000000　　# 行数
mean     180921.195890　　# 平均值
std       79442.502883　　# 标准差
min       34900.000000　　# 最小值
25%      129975.000000　　# 第1四分位数，即第25百分位数
50%      163000.000000　　# 第2四分位数，即第50百分位数
75%      214000.000000　　# 第3四分位数，即第75百分位数
max      755000.000000　　# 最大值
Name: SalePrice, dtype: float64

使用displot函数可以绘制直方图，bins越大，横坐标的精度越大

1
2
3
4
5
6
7
8
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

sns.displot(train_data['SalePrice'], bins=100)
plt.show()

可以看到数据呈现偏态分布

2.双变量关系可视化

使用scatterplot函数绘制散点图，查看2个数值型（numerical）变量的关系

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
import seaborn as sns

# 地上居住面积/房价散点图
sns.scatterplot(y=train_data['SalePrice'], x=train_data['GrLivArea'])
plt.show()
# 或者
data = pd.concat([train_data['SalePrice'], train_data['GrLivArea']], axis=1) 
data.plot.scatter(x='GrLivArea', y='SalePrice', ylim=(0, 800000)) 
plt.show()

可以看出面积越大的房子，价格越高

全文 >>

机器学习——预测数值型数据：回归

tonglin0325

线性回归

优点：结果易于理解，计算上不复杂

缺点：对非线性的数据拟合不好

适用数据类型：数值型和标称型数据

 

回归的目的就预测数值型的目标值。最直接的办法就是依据输入写一个目标值的计算公式。这个计算公式就是所谓的回归方程(regression equation)，其中的参数就是回归系数，求这些回归系数的过程就是回归。

　　说道回归，一般都是指线性回归（linear regression）。

给定由d个属性描述的示例 ，其中xi是x在第i个属性上的取值，线性模型试图学得一个通过属性组合来进行预测的函数，即

**　　**

 

一般用向量形式写成

**　　**

其中w={w1;w2;…;wd}，w和b学得之后，模型就得以确定。

 

更加一般的情况是，给定一个数据集** **，其中 ，“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。

用向量形式写成

**　　，这称为“多元线性回归”**

 

因为是d维的特性，那么w就是一个由回归系数组成的d×1维向量，X是n×（d+1）的矩阵（第一列元素都是1，其余列都是x1…xn），是（d+1）×1的向量

全文 >>

机器学习——非均衡分类问题

tonglin0325

在机器学习的分类问题中，我们都假设所有类别的分类代价是一样的。但是事实上，不同分类的代价是不一样的，比如我们通过一个用于检测患病的系统来检测马匹是否能继续存活，如果我们把能存活的马匹检测成患病，那么这匹马可能就会被执行安乐死；如果我们把不能存活的马匹检测成健康，那么就会继续喂养这匹马。一个代价是错杀一只昂贵的动物，一个代价是继续喂养，很明显这两个代价是不一样的。

1.性能度量

衡量模型泛化能力的评价标准，就是性能度量。除了基于错误率来衡量分类器任务的成功程度的。错误率指的是在所有测试样例中错分的样例比例。但是，这样却掩盖了样例如何被错分的事实。在机器学习中，有一个普遍试用的称为混淆矩阵（confusion matrix）的工具，可以帮助人们更好地了解分类的错误。

利用混淆矩阵就可以更好地理解分类中的错误了。如果矩阵中的非对角元素均为0，就会得到一个完美的分类器。

2.正确率（Precision）、召回率（Recall）

正确率P = TP/（TP+FP），给出的是预测为正例的样本中的真正正例的比例。

召回率R = TP/（TP+FN），给出的是预测为正例的真实正例占所有真实正例的比例。

3.ROC曲线

另一个用于度量分类中的非均衡性的工具是ROC曲线（ROC curve），ROC代表接收者操作特征”Receiver Operating Characteristic”

ROC曲线的纵轴是“真正例率”，TPR=TP/（TP+FN）

横轴是“假正例率”，FPR=FP/（TN+FP）

在理想的情况下，最佳的分类器应该尽可能地处于左上角，这就意味着分类器在假正例率很低的同时，获得了很高的真正例率。

4.AUC（曲线下的面积）

对不同的ROC曲线进行比较的一个指标就是曲线下的面积（AUC），AUC给出的是分类器的平均性能值。一个完美的分类器的AUC是1，而随机猜测的AUC则为0.5。

若一个学习器的ROC曲线能把另一个学习器的ROC曲线完全包住，则这个学习器的性能比较好。

全文 >>

git命令

tonglin0325

cd到需要git的目录

初始化git仓库

1
2
3
git init
git remote add origin git@github.com:tonglin0325/XXX.git

新建分支

1
2
git checkout -b testing

添加并转到testing分支，不要直接在master分支上操作

1
2
git branch -d testing

 

撤销一次commit

1
2
git reset --soft HEAD^

全文 >>

网络抓包wireshark（转）

tonglin0325

ubuntu下非root用户下获得使用wireshark的权限

在非root用户下不能使用wireshark用来抓包，所以需要进行以下操作：

1
2
3
4
5
sudo groupadd  wireshark
sudo chgrp wireshark /usr/bin/dumpcap
sudo chmod 4755 /usr/bin/dumpcap
sudo gpasswd -a common wireshark

抓包应该是每个技术人员掌握的基础知识，无论是技术支持运维人员或者是研发，多少都会遇到要抓包的情况，用过的抓包工具有fiddle、wireshark，作为一个不是经常要抓包的人员，学会用Wireshark就够了，毕竟它是功能最全面使用者最多的抓包工具。

Wireshark（前称Ethereal）是一个网络封包分析软件。网络封包分析软件的功能是撷取网络封包，并尽可能显示出最为详细的网络封包资料。Wireshark使用WinPCAP作为接口，直接与网卡进行数据报文交换。

wireshark的官方下载网站： http://www.wireshark.org/

wireshark是非常流行的网络封包分析软件，功能十分强大。可以截取各种网络封包，显示网络封包的详细信息。

wireshark是开源软件，可以放心使用。 可以运行在Windows和Mac OS上。

Wireshark不能做的

为了安全考虑，wireshark只能查看封包，而不能修改封包的内容，或者发送封包。

Wireshark VS Fiddler

wireshark能获取HTTP，也能获取HTTPS，但是不能解密HTTPS，所以wireshark看不懂HTTPS中的内容

同类的其他工具

sniffer

全文 >>

使用openssl生成自签名ssl证书

tonglin0325

使用自签名的证书的网站默认不会被浏览器信任，使用浏览器带打开可能会弹出如下界面，需要在浏览器中点击继续前往或者添加例外

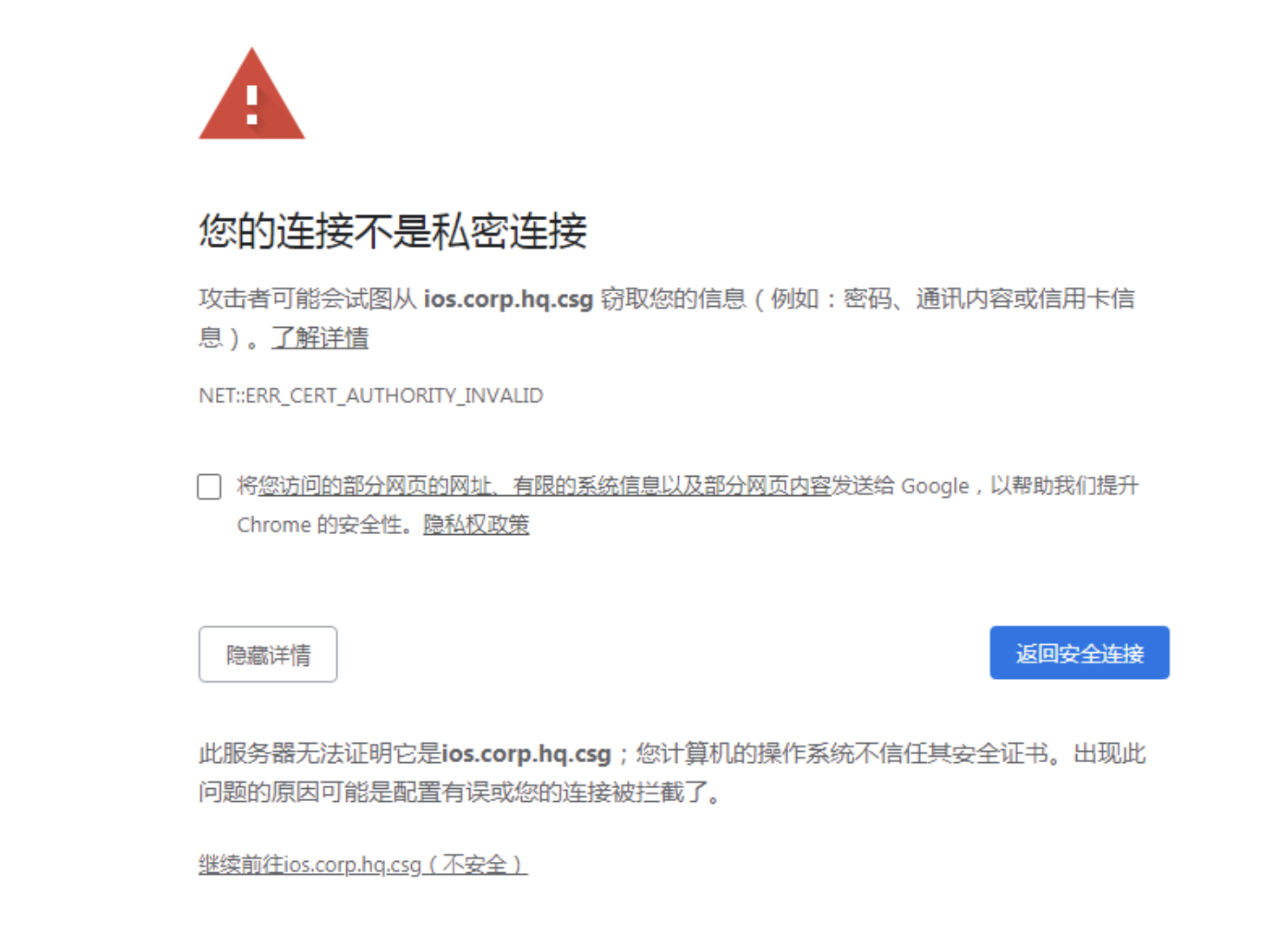
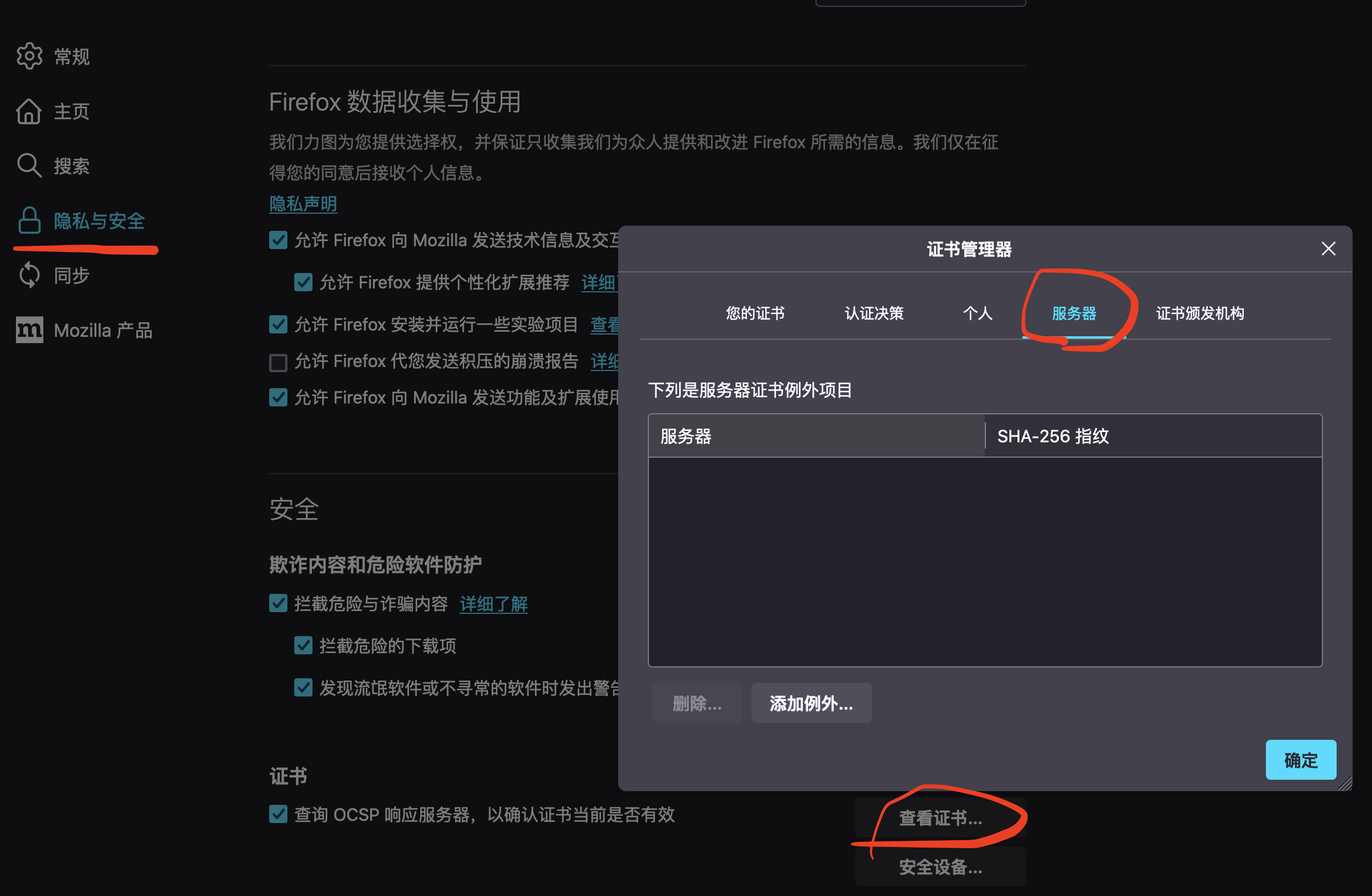
添加的例外可以在Firefox浏览器中如下界面中设置——隐私与安全——证书中进行查看

生成CA私钥

ca.key是证书颁发机构（Certificate Authority，CA）的私钥文件，CA私钥用于签署证书并保护证书颁发机构的安全性。

1
2
openssl genrsa -out ca.key 2048

生成CA证书

ca.crt是证书颁发机构（Certificate Authority，CA）的证书文件，CA证书用于签名其他证书，验证证书的合法性。

1
2
3
# 20 年有效期
openssl req -x509 -new -nodes -key ca.key -sha256 -days 7300 -out ca.crt

生成服务器ssl证书私钥

server.key是服务器私钥，用于生成服务器证书、加密通信和验证身份。

1
2
openssl genrsa -out server.key 2048

全文 >>

ubuntu16.04下Jenkins使用

tonglin0325

1.安装

1
2
sudo apt-get install jenkins=2.249.2

修改端口

1
2
3
4
sudo vim /etc/default/jenkins

HTTP_PORT=10001

参考

1
2
https://www.jenkins.io/doc/book/installing/linux/#debianubuntu

以及

ubuntu安装Jenkins及修改端口

 

2.新建Jenkins任务，使用参考

1
2
https://github.com/muyinchen/woker/blob/master/%E9%9B%86%E6%88%90%E6%B5%8B%E8%AF%95%E7%8E%AF%E5%A2%83%E6%90%AD%E5%BB%BA/%E6%89%8B%E6%8A%8A%E6%89%8B%E6%95%99%E4%BD%A0%E6%90%AD%E5%BB%BAJenkins%2BGithub%E6%8C%81%E7%BB%AD%E9%9B%86%E6%88%90%E7%8E%AF%E5%A2%83.md

创建一个item

全文 >>

机器学习-损失函数 （转）

tonglin0325

参考

1
2
3
作者：刘帝伟
原文地址：http://www.csuldw.com/

 

损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子：

　　　　

一、log对数损失函数（逻辑回归）

有些人可能觉得逻辑回归的损失函数就是平方损失，其实并不是。平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到，而逻辑回归得到的并不是平方损失。在逻辑回归的推导中，它假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值等等。而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为：**最小化负的似然函数（即max F(y, f(x)) —-> min -F(y, f(x)))**。从损失函数的视角来看，它就成了log损失函数了。

log损失函数的标准形式：L(Y,P(Y|X))=−log⁡P(Y|X)“><br>

      
刚刚说到，取对数是为了方便计算极大似然估计，因为在MLE中，直接求导比较困难，所以通常都是先取对数再求导找极值点。损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下，使概率P(Y|X)达到最大值（换言之，就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说什么样的参数才能使我们观测到目前这组数据的概率最大）。因为log函数是单调递增的，所以logP(Y|X)也会达到最大值，因此在前面加上负号之后，最大化P(Y|X)就等价于最小化L了。

逻辑回归的P(Y=y|x)表达式如下（为了将类别标签y统一为1和0，下面将表达式分开表示）：

　　　　

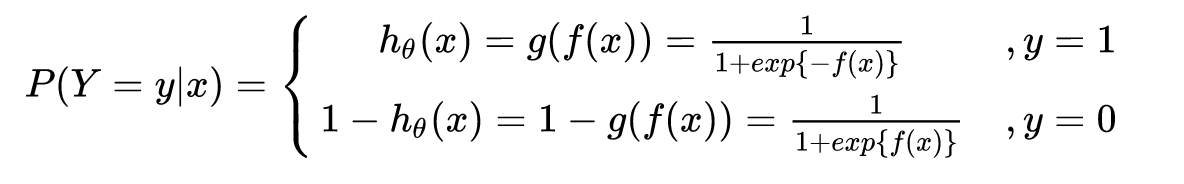
将它带入到上式，通过推导可以得到logistic的损失函数表达式，如下：

　　　　

全文 >>

机器学习——AdaBoost元算法

tonglin0325

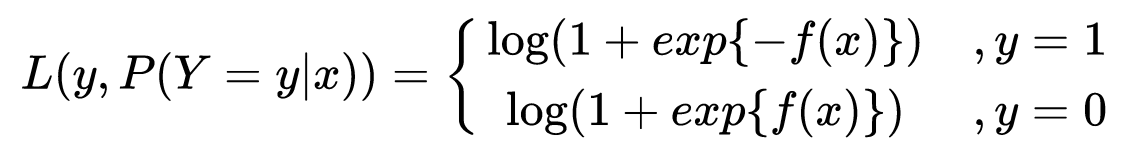
当做重要决定时，我们可能会考虑吸取多个专家而不只是一个人的意见。机器学习处理问题也是这样，这就是元算法（meta-algorithm）背后的思路。

**　　元算法是对其他算法进行组合的一种方式，其中最流行的一种算法就是AdaBoost算法。某些人认为AdaBoost是最好的监督学习的方法**，所以该方法是机器学习工具箱中最强有力的工具之一。

　　集成学习或者元算法的一般结构是：先产生一组**“个体学习器”，再用某种策略将他们结合起来。个体学习器**通常是由一个现有的学习算法从训练数据产生。

　　根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类，即

　　1.个体学习器间存在强依赖关系、必须串行生成的序列化方法，典型的代表是Boosting，其中AdaBoost就是Boosting的最流行的一个版本

　　2.个体学习器间不存在强依赖关系、可同时生成的并行化方法，典型的代表是Bagging和“随机森林”（Random Forest）

 

AdaBoost

优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整

缺点：对离群点敏感

使用数据类型：数值型和标称型数据

 

bagging：基于数据随机重抽样的分类器构建方法

自举汇聚法（bootstrap aggregating），也称为bagging方法，它直接基于自助采样法（bootstrap samping）。

给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中，这样，经过m次随机采样操作，我们得到了含m个样本的采样集。这样从原始数据集选择T次后得到T个新数据集，且每个新数据集的大小和原数据集的大小相等。在T个新数据集建好之后，将某个学习算法分别作用于每个数据集就得到了T个分类器。当我们要对新数据集进行分类时，就可以应用这T个分类器进行分类。与此同时，选择分类器投票结果中最多的类别作为最后的分类结果（权重相等）。

 

Boosting

boosting是一种和bagging很类似的技术。其使用的多个分类器的类型都是一致的。

在boosting中，不同的分类器是通过串行训练而获得的，每个新分类器都根据已训练出的分类器的性能来进行训练。boosting是通过集中关注被已有分类器错分的那些数据来获得新的分类器。

boosting分类的结果是基于所有分类器的加权求和结果的，在bagging中的分类器权重是相等的，而boosting中的分类器权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。

 

全文 >>

机器学习——支持向量机(SVM)之核函数(kernel)

tonglin0325

对于线性不可分的数据集，可以利用核函数（kernel）将数据转换成易于分类器理解的形式。

　　如下图，如果在x轴和y轴构成的坐标系中插入直线进行分类的话， 不能得到理想的结果，或许我们可以对圆中的数据进行某种形式的转换，从而得到某些新的变量来表示数据。在这种表示情况下，我们就更容易得到大于0或者小于0的测试结果。在这个例子中，我们将数据从一个特征空间转换到另一个特征空间，在新的空间下，我们可以很容易利用已有的工具对数据进行处理，将这个过程称之为从一个特征空间到另一个特征空间的映射。在通常情况下，这种映射会将低维特征空间映射到高维空间。

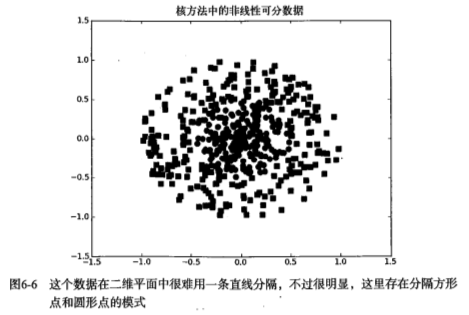
　　这种从某个特征空间到另一个特征空间的映射是通过核函数来。

　　SVM优化中一个特别好的地方就是，所有的运算都可以写成内积（inner product）的形式。向量的内积指的就是两个向量相乘，之后得到单个标量或者数值。我们可以把内积运算替换成核函数，而并不必做简化处理。将内积替换成核函数的方法被称之为核技巧（kernel trick）或者核“变电”（kernel substation）。

 

径向基核函数

径向基核函数是SVM中常用的一个核函数。径向基函数是一个采用向量作为自变量的函数，能够基于向量距离运算输出一个标量。

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
'''#######********************************
以下是有核函数的版本
'''#######********************************
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters 
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #first column is valid flag
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
        
def calcEk(oS, k):			#计算误差
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek
        
def selectJ(i, oS, Ei):         	#用于选择第2个循环（内循环）的alpha值，内循环中的启发式方法
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]  		#set valid #choose the alpha that gives the maximum delta E
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   	#loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue 	#跳过本身
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):	#选取具有最大步长的j
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEk(oS, k):			#alpha改变后，更新缓存
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]
        
#内部循环的代码和简版的SMO代码很相似
def innerL(i, oS):		
    Ei = calcEk(oS, i)
    #判断每一个alpha是否被优化过，如果误差很大，就对该alpha值进行优化，toler是容错率
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) 			#使用启发式方法选取第2个alpha，选取使得误差最大的alpha
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        #保证alpha在0与C之间
        if (oS.labelMat[i] != oS.labelMat[j]):		#当y1和y2异号，计算alpha的取值范围 
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:						#当y1和y2同号，计算alpha的取值范围
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: print "L==H"; return 0
	#eta是alpha[j]的最优修改量，eta=K11+K22-2*K12,也是f(x)的二阶导数，K表示核函数
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] 	#changed for kernel
        #如果二阶导数-eta <= 0，说明一阶导数没有最小值，就不做任何改变，本次循环结束直接运行下一次for循环
        if eta >= 0: print "eta>=0"; return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta	#利用公式更新alpha[j]，alpha2new=alpha2-yj(Ei-Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)	#判断alpha的范围是否在0和C之间
        updateEk(oS, j) 				#在alpha改变的时候更新Ecache
        print "j=",j
        print oS.alphas.A[j]
        #如果alphas[j]没有调整，就忽略下面语句，本次循环结束直接运行下一次for循环
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) 				#在alpha改变的时候更新Ecache                   
        print "i=",i
        print oS.alphas.A[i]     
        #已经计算出了alpha，接下来根据模型的公式计算b   
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        #根据公式确定偏移量b，理论上可选取任意支持向量来求解，但是现实任务中通常使用所有支持向量求解的平均值，这样更加鲁棒
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1		#如果有任意一对alpha发生改变，返回1
    else: return 0

#完整版Platt SMO的外循环
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):	#有alpha改变同时遍历次数小于最大次数，或者需要遍历整个集合
        alphaPairsChanged = 0
        #首先进行完整遍历，过程和简化版的SMO一样
        if entireSet:   	
            for i in range(oS.m):        
                alphaPairsChanged += innerL(i,oS)		#i是第1个alpha的下标
                print "完整遍历, 迭代次数: %d i:%d, 成对改变的次数 %d" % (iter,i,alphaPairsChanged)
            iter += 1
        #非边界遍历，挑选其中alpha值在0和C之间非边界alpha进行优化 
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]	#然后挑选其中值在0和C之间的非边界alpha进行遍历
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print "非边界, 迭代次数: %d i:%d, 成对改变的次数 %d" % (iter,i,alphaPairsChanged)
            iter += 1
        #如果这次是完整遍历的话，下次不用进行完整遍历
        if entireSet: entireSet = False 			#终止完整循环
        elif (alphaPairsChanged == 0): entireSet = True  	#如果alpha的改变数量为0的话，再次遍历所有的集合一次
        print "iteration number: %d" % iter
    return oS.b,oS.alphas

def calcWs(alphas,dataArr,classLabels):		#计算模型的参数w，即alpha*y*x转置的累加
    X = mat(dataArr); labelMat = mat(classLabels).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w

def testRbf(k1=1.3):
    dataArr,labelArr = loadDataSet('testSetRBF.txt')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] #get matrix of only support vectors
    labelSV = labelMat[svInd];
    print "there are %d Support Vectors" % shape(sVs)[0]
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print "the training error rate is: %f" % (float(errorCount)/m)
    dataArr,labelArr = loadDataSet('testSetRBF2.txt')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print "the test error rate is: %f" % (float(errorCount)/m)    
    
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9: hwLabels.append(-1)
        else: hwLabels.append(1)
        trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels    

def testDigits(kTup=('rbf', 10)):
    dataArr,labelArr = loadImages('trainingDigits')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] 
    labelSV = labelMat[svInd];
    print "there are %d Support Vectors" % shape(sVs)[0]
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print "the training error rate is: %f" % (float(errorCount)/m)
    dataArr,labelArr = loadImages('testDigits')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print "the test error rate is: %f" % (float(errorCount)/m)

 

全文 >>

tonglin0325

标签

标签云

AWS Airbnb Android CDH Doris ELK Flink Git Grafana HAProxy HBase Hadoop Hive Hudi InfluxDB JDBC JMeter JVM Java LaTex Linkedin Linux ML ML Infra MPP Maven MySQL Nexus OpenTSDB Paper Play Prometheus Python React Redis RocksDB Scala Solr Spark SpringBoot SpringMVC Thrift YARN antlr arthas avro cassandra clickhouse confluent docker filebeat flume golang google gradle hexo impala jenkins k8s kafka kerberos kudu ldap mac mongo mybatis nginx nlp open-falcon openwrt parquet presto ranger rocketmq scyllaDB twitter zookeeper 刷题 前端 图存储及计算 多线程 广告系统 开发工具 数据结构 杂谈 算法 系统设计 计算机基础 设计模式

文章归档

最近文章