机器学习——AdaBoost元算法

当做重要决定时，我们可能会考虑吸取多个专家而不只是一个人的意见。机器学习处理问题也是这样，这就是元算法（meta-algorithm）背后的思路。

**　　元算法是对其他算法进行组合的一种方式，其中最流行的一种算法就是AdaBoost算法。某些人认为AdaBoost是最好的监督学习的方法**，所以该方法是机器学习工具箱中最强有力的工具之一。

　　集成学习或者元算法的一般结构是：先产生一组**“个体学习器”，再用某种策略将他们结合起来。个体学习器**通常是由一个现有的学习算法从训练数据产生。

　　根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类，即

　　1.个体学习器间存在强依赖关系、必须串行生成的序列化方法，典型的代表是Boosting，其中AdaBoost就是Boosting的最流行的一个版本

　　2.个体学习器间不存在强依赖关系、可同时生成的并行化方法，典型的代表是Bagging和“随机森林”（Random Forest）

 

AdaBoost

优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整

缺点：对离群点敏感

使用数据类型：数值型和标称型数据

 

bagging：基于数据随机重抽样的分类器构建方法

自举汇聚法（bootstrap aggregating），也称为bagging方法，它直接基于自助采样法（bootstrap samping）。

给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中，这样，经过m次随机采样操作，我们得到了含m个样本的采样集。这样从原始数据集选择T次后得到T个新数据集，且每个新数据集的大小和原数据集的大小相等。在T个新数据集建好之后，将某个学习算法分别作用于每个数据集就得到了T个分类器。当我们要对新数据集进行分类时，就可以应用这T个分类器进行分类。与此同时，选择分类器投票结果中最多的类别作为最后的分类结果（权重相等）。

 

Boosting

boosting是一种和bagging很类似的技术。其使用的多个分类器的类型都是一致的。

在boosting中，不同的分类器是通过串行训练而获得的，每个新分类器都根据已训练出的分类器的性能来进行训练。boosting是通过集中关注被已有分类器错分的那些数据来获得新的分类器。

boosting分类的结果是基于所有分类器的加权求和结果的，在bagging中的分类器权重是相等的，而boosting中的分类器权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。

 

现在介绍其中的AdaBoost

 

弱分类器的“弱”意味着分类器的性能比随机猜测要略好，但是也不会好太多。这就是说，在二分类情况下，弱分类器的错误率会高于50%，而强分类器的错误率会低很多。

AdaBoost是adaptive boosting（自适应boosting）的缩写，其运行过程如下：

假设一个二类分类的训练数据集

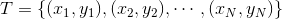
<1>训练数据中的每个样本，并赋予其一个权重，这些权重构成了初始向量D。一开始，这些权重都初始化成相等值。

 

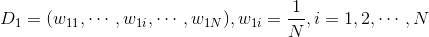
AdaBoost算法多种推导方式，比较容易理解的是基于“加性模型”，即基学习器的线性组合

　　，其中 为基学习器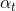， 为系数

来最小化指数损失函数（exponential loss function），损失函数见 机器学习-损失函数 （转）

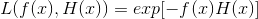**　　 ，其中f(x)是正确的分类，等于-1或者1，H(x)是分类器的分类结果，等于-1或者1**

**　　**

　　　　　　　　　　　　

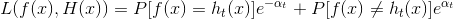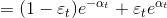
，所以对该式子求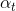的偏导，得 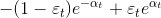，并令其等于0，得

**　　　**

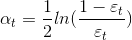<2>首先在训练分类器上训练出一个弱分类器并计算该分类的错误率，然后在同一数据集上再次训练弱分类器。

在分类器的第二次训练中，将会重新调整每个样本的权重，其中第一次分对的样本的权重将会降低，而第一次分错的样本的权重将会提高。为了从所有弱分类器中得到最终的分类结果，AdaBoost为每个分类器都分配了一个权重值alpha，这些alpha值是基于每个弱分类器的错误率进行计算的。

其中，错误率 的定义为

　　= 为正确分类的样本数目/所有样本数目

而alpha的计算公式如下：

　　

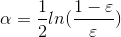
计算出alpha值之后，可以对权重向量D进行更新，以使得那些正确分类的样本的权重降低而错分样本的权重升高。D的计算方法如下：

　　 

其中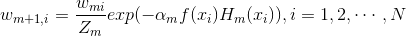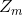，，是规范化因子

　　

它使得成为一个概率分布

如果某个样本被正确分类，那么该样本的权重更改为

　　

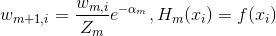
如果某个样本被错误分类，那么该样本的权重更改为

　　

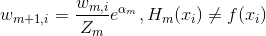
在计算出D之后，AdaBoost算法又开始进入下一轮迭代。

AdaBoost算法会不断地重复训练和调整权重的过程，直到训练错误率为0或者弱分类器的数目达到用户的指定值为止。

 

from numpy import *

def loadSimpData():
    datMat = matrix([[ 1. ,  2.1],
        [ 1.5,  1.6],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels

 

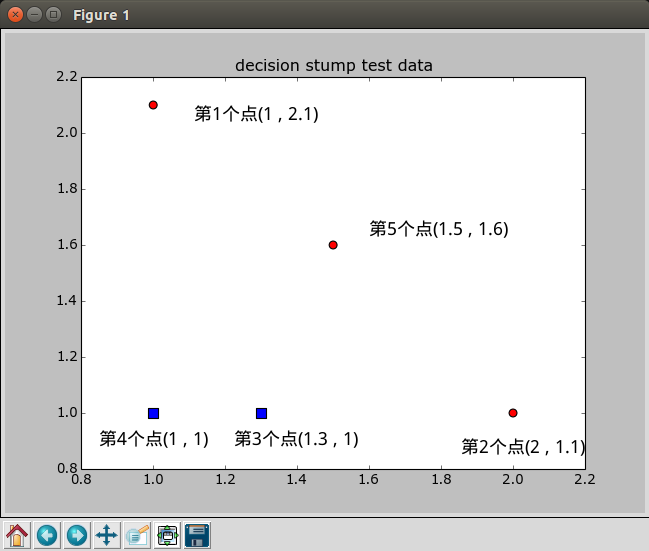
def plotBestFit(weakClassArr):		#画出数据集和所有的基学习器
	#import matplotlib.pyplot as plt
	dataMat,labelMat=loadSimpData()	#数据矩阵和标签向量
	dataArr = array(dataMat)		#转换成数组
	n = shape(dataArr)[0] 
	xcord1 = []; ycord1 = []		#声明两个不同颜色的点的坐标
	xcord2 = []; ycord2 = []
	for i in range(n):
		if int(labelMat[i])== 1:
			xcord1.append(dataArr[i,0]); ycord1.append(dataArr[i,1])
		else:
			xcord2.append(dataArr[i,0]); ycord2.append(dataArr[i,1])
	fig = plt.figure()
	ax = fig.add_subplot(111)
	ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
	ax.scatter(xcord2, ycord2, s=30, c='green')
	print "weakClassArr[0]['thresh']",weakClassArr[0]['dim']
	for j in range(len(weakClassArr)):
		if(weakClassArr[j]['dim'] == 1):
			x = arange(-0.0, 2.5, 0.1)
			y = x*0+weakClassArr[j]['thresh']
			ax.plot(x, y)
		else:
			y = array(arange(-0.0, 2.5, 0.1))
			x = y*0+weakClassArr[j]['thresh']
			ax.plot(x, y)
	plt.xlabel('X1'); plt.ylabel('X2');
	plt.show()

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):	#通过阈值比较对数据进行分类
    retArray = ones((shape(dataMatrix)[0],1))				#首先将返回的数组的全部元素设置为1
    if threshIneq == 'lt':
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0	#将满足<=不等式的元素设为-1
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0	#将满足>不等式的元素设为-1
    return retArray
    

def buildStump(dataArr,classLabels,D):		#遍历stumpClassify()函数所有的可能输入值，并找到数据集上最佳的单层决策树
    dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
    m,n = shape(dataMatrix)					#m=5,n=2
    numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
    minError = inf 							#初始误差总和，为无穷大
    for i in range(n):						#循环X和Y两个维度
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();		#取得X和Y两个维度的最大值和最小值特征
        stepSize = (rangeMax-rangeMin)/numSteps									#步进长度
        for j in range(-1,int(numSteps)+1):				#从-1到10步进
            for inequal in ['lt', 'gt']: 				#"lt"为满足<=不等式，"gt"为满足>不等式
                threshVal = (rangeMin + float(j) * stepSize)					#当前阈值
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)	#根据阈值和不等式，计算预测的分类
                errArr = mat(ones((m,1)))
                errArr[predictedVals == labelMat] = 0	#样本估计错误的标记为1
                weightedError = D.T*errArr  			#通过权重和错误标记，计算泛化误差
                #print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
                if weightedError < minError:			#如果泛化误差是最小的
                    minError = weightedError
                    bestClasEst = predictedVals.copy()	#保存最佳预测结果
                    bestStump['dim'] = i				#保存维度、阈值、不等式符号
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst


def adaBoostTrainDS(dataArr,classLabels,numIt=40):	#基于单层决策树的AdaBoost训练
    weakClassArr = []
    m = shape(dataArr)[0]							#需要分类的数据量，m=5
    D = mat(ones((m,1))/m)   						#D为权重向量，初始D1...D5的和等于1
    aggClassEst = mat(zeros((m,1)))					#基分类器的线性组合
    for i in range(numIt):
	    #建立单层决策树，bestStump包括维度，不等式，阈值，error泛化误差，classEst是每个基分类器
        bestStump,error,classEst = buildStump(dataArr,classLabels,D)	
        print "最佳决策树=",bestStump,"泛化误差=",error,"更新前的分类器预测结果=",classEst.T 
        #print "D:",D.T
        alpha = float(0.5*log((1.0-error)/max(error,1e-16)))	#根据泛化误差，计算基分类器的权重&alpha;值
        bestStump['alpha'] = alpha  							#把权重&alpha;值添加到最佳决策树的列表中
        print "最佳决策树=",bestStump
        weakClassArr.append(bestStump)                  		#保存单层最佳决策树参数到数组中
        print "预测分类: ",classEst.T
        expon = multiply(-1*alpha*mat(classLabels).T,classEst) 	#权重&alpha;&times;真实分类&times;预测分类，multiply为对应元素相乘，不是矩阵相乘
        D = multiply(D,exp(expon))                              #Calc New D for next iteration
        D = D/D.sum()											#更新D,D.sum()为规范化因子
        #calc training error of all classifiers, if this is 0 quit for loop early (use break)
        aggClassEst += alpha*classEst
        print "更新后的分类器预测结果: ",aggClassEst.T
        aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))	#boolean值和1相乘
        errorRate = aggErrors.sum()/m												#计算错误率
        print "total error: ",errorRate
        if errorRate == 0.0: break
    return weakClassArr,aggClassEst

def adaClassify(datToClass,classifierArr):			#AdaBoost分类函数
    dataMatrix = mat(datToClass)					#输入[0,0]转换成[[0,0]]矩阵
    m = shape(dataMatrix)[0]
    aggClassEst = mat(zeros((m,1)))
    for i in range(len(classifierArr)):
        classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
                                 classifierArr[i]['thresh'],\
                                 classifierArr[i]['ineq'])				#维度、阈值、不等式符号
        aggClassEst += classifierArr[i]['alpha']*classEst				#计算在每一个基分类器上的预测值的累加和
        print "aggClassEst=",aggClassEst
    return sign(aggClassEst)

 

main.py

# coding:utf-8
# !/usr/bin/env python

import adaboost

if __name__ == '__main__':
	datMat,classLabels = adaboost.loadSimpData()
	weakClassArr,aggClassEst = adaboost.adaBoostTrainDS(datMat,classLabels)
	print "弱分类器组合:",weakClassArr
	print adaboost.adaClassify([[0,0],[5,5]],weakClassArr)
	adaboost.plotBestFit(weakClassArr)

 

1个分类器————　　　　　　　　　　　　2个分类器————　　　　　　　　　　　　3个分类器————