1.哈夫曼树#
给定N个权值作为N个叶子节点，构造一棵二叉树，若该树的带权路径长度****（WPL）达到最小，称这样的二叉树为最优二叉树，也称为**哈夫曼树(Huffman Tree)**。
哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
参考：霍夫曼树（参考该文章中的概念，其中代码不对）
2.树的带权路径长度（WPL，Weighted Path Length of Tree）#
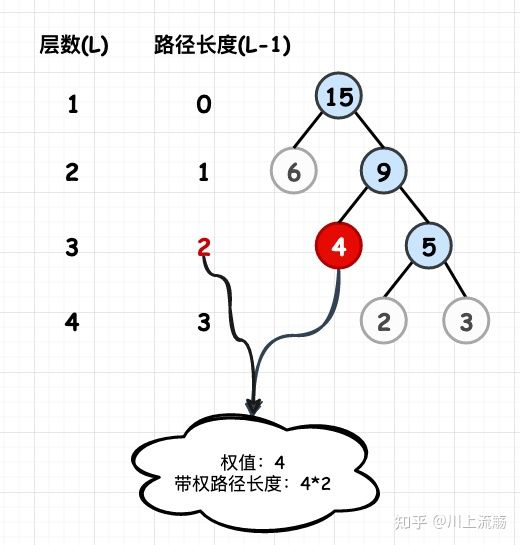
树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）
如下图中的哈夫曼树，其WPL的值 = (2+3) * 3 + 4 * 2 + 6 * 1 = 29
3.哈夫曼树的应用#
1.哈夫曼编码#
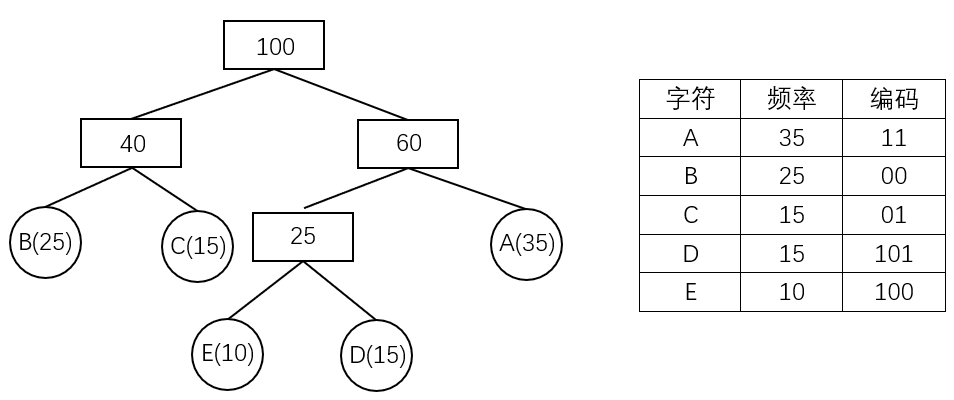
4.哈夫曼编码的实现#
1.哈夫曼编码的步骤：#
-
1. 统计原始数据中各字符出现的频率；
1. 所有字符按频率降序排列；
1. 建立哈夫曼树：
- 将哈夫曼树存入结果数据；
- 重新编码原始数据到结果数据
- 初始化：由给定的 N
个权值构造 N 棵只有一个根节点的二叉树，得到一个二叉树集合 。 - 选取与合并：从二叉树集合 PriorityQueue 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
- 删除与加入：从 PriorityQueue 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 PriorityQueue 中。
- 重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。
2.建立哈夫曼树的步骤：#
3.代码实现：#
下面的2个网站中的实现都差不多，都借助了优先队列来进行排序（java是PriorityQueue，python是heapq）
