tonglin0325的个人主页

机器学习——决策树

tonglin0325

1.决策树的构造

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据

缺点：可能会产生过度匹配问题

适用数据类型：数值型和标称型

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
# coding:utf-8
# !/usr/bin/env python

'''
Created on Oct 12, 2010
Decision Tree Source Code for Machine Learning in Action Ch. 3
@author: Peter Harrington
'''
from math import log
import operator

#通过是否浮出水面和是否有脚蹼，来划分鱼类和非鱼类
def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

def calcShannonEnt(dataSet):	#计算给定数据集的香农熵
    numEntries = len(dataSet)	#数据集中的实例总数
    labelCounts = {}
    #为所有可能的分类创建字典，键是可能的特征属性，值是含有这个特征属性的总数
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #计算香农熵
    shannonEnt = 0.0
    #为所有的分类计算香农熵
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) 	#以2为底求对数
    #香农熵Ent的值越小，纯度越高，即通过这个特征属性来分类，属于同一类别的结点会比较多
    return shannonEnt
    
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
    
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy
        if (infoGain > bestInfoGain):       #compare this to the best gain so far
            bestInfoGain = infoGain         #if better than current best, set to best
            bestFeature = i
    return bestFeature                      #returns an integer

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]#stop splitting when all of the classes are equal
    if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       #copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree                            
    
def classify(inputTree,featLabels,testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

def storeTree(inputTree,filename):
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()
    
def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)
    
    
if __name__ == '__main__':
    myDat,labels = createDataSet()
    print myDat
    print calcShannonEnt(myDat)

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#通过是否浮出水面和是否有脚蹼，来划分鱼类和非鱼类
def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    #change to discrete values
    return dataSet, labels

def calcShannonEnt(dataSet):	#计算给定数据集的香农熵
    numEntries = len(dataSet)	#数据集中的实例总数
    labelCounts = {}
    #为所有可能的分类创建字典，键是可能的特征属性，值是含有这个特征属性的总数
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #计算香农熵
    shannonEnt = 0.0
    #为所有的分类计算香农熵
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) 	#以2为底求对数
    #香农熵Ent的值越小，纯度越高，即通过这个特征属性来分类，属于同一类别的结点会比较多
    return shannonEnt

 

1
2
3
4
myDat,labels = createDataSet()
print myDat
print calcShannonEnt(myDat)

 

 

2.划分数据集

1
2
3
4
5
6
7
8
9
10
def splitDataSet(dataSet, axis, value):		#按照给定特征划分数据集，axis表示根据第几个特征，value表示特征的值
    retDataSet = []				#创建新的list对象
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     #切片
            reducedFeatVec.extend(featVec[axis+1:])	#把序列添加到列表reducedFeatVec中
            #print reducedFeatVec
            retDataSet.append(reducedFeatVec)		#把对象reducedFeatVec（是一个list）添加到列表retDataSet中
    return retDataSet

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def chooseBestFeatureToSplit(dataSet):		#选择最好的数据集划分方式
    numFeatures = len(dataSet[0]) - 1      	#特征的数量，最后一列是标签，所以减去1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1	#信息增益和最好的特征下标
    for i in range(numFeatures):        	#递归所有特征
        featList = [example[i] for example in dataSet]	#创建一个列表，包含第i个特征的所有值
        uniqueVals = set(featList)       	#创建一个集合set，由不同的元素组成
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)	#按照所有特征的可能划分数据集
            prob = len(subDataSet)/float(len(dataSet))		#计算所有特征的可能性
            newEntropy += prob * calcShannonEnt(subDataSet)     
        infoGain = baseEntropy - newEntropy     #计算信息增益
        if (infoGain > bestInfoGain):       	#比较不同特征之间信息增益的大小
            bestInfoGain = infoGain         	#选取信息增益大的特征
            bestFeature = i
    return bestFeature                      	#返回特征的下标

 

3.递归构建决策树

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def createTree(dataSet,labels):		#创建决策树的函数，采用字典的表示形式
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 	#如果类别完全相同则停止继续划分
        return classList[0]
    if len(dataSet[0]) == 1: 					#遍历完所有特征时返回出现次数最多的
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)		#选择信息增益最大的特征下标
    bestFeatLabel = labels[bestFeat]				#选择信息增益最大的特征
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])					#从标签中删除已经划分好的特征
    featValues = [example[bestFeat] for example in dataSet]	#取得该特征的所有可能取值
    uniqueVals = set(featValues)				#建立一个集合
    for value in uniqueVals:
        subLabels = labels[:]       
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)	#递归createTree
    return myTree

 

1
2
3
4
5
6
myDat,labels = createDataSet()
myTree = createTree(myDat,labels)
print myTree

{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

 

 

4.在Python中使用Matplotlib注解绘制树形图

1
2
3
4
5
myDat,labels = createDataSet()
print myDat
import treePlotter
treePlotter.createPlot(myTree)　　#绘制树形图

 

 

5.构造注解树

 获取叶节点的数目和树的层数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import matplotlib.pyplot as plt

decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")

def getNumLeafs(myTree):		#获取叶子节点的数目
    numLeafs = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#测试节点的数据类型是否为字典
            numLeafs += getNumLeafs(secondDict[key])	#递归
        else:   numLeafs +=1				#如果不是字典，则说明是叶子节点
    return numLeafs

def getTreeDepth(myTree):		#获取树的层数
    maxDepth = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#测试节点的数据类型是否为字典，如果不是字典，则说明是叶子节点
            thisDepth = 1 + getTreeDepth(secondDict[key])	#递归
        else:   thisDepth = 1				
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

 绘制树形图

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
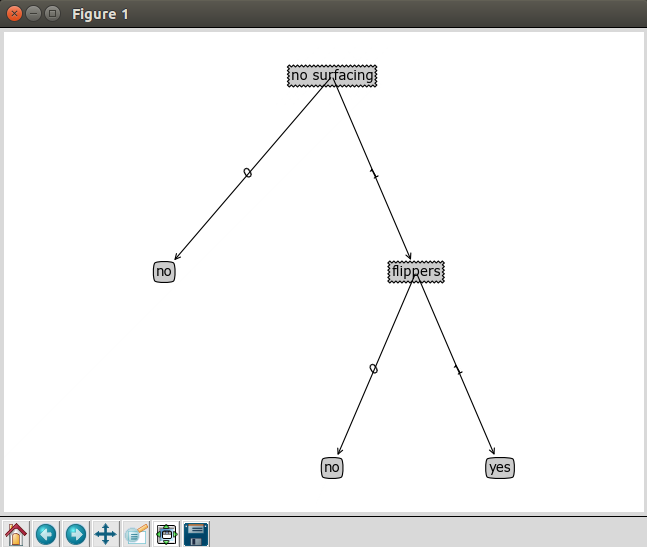
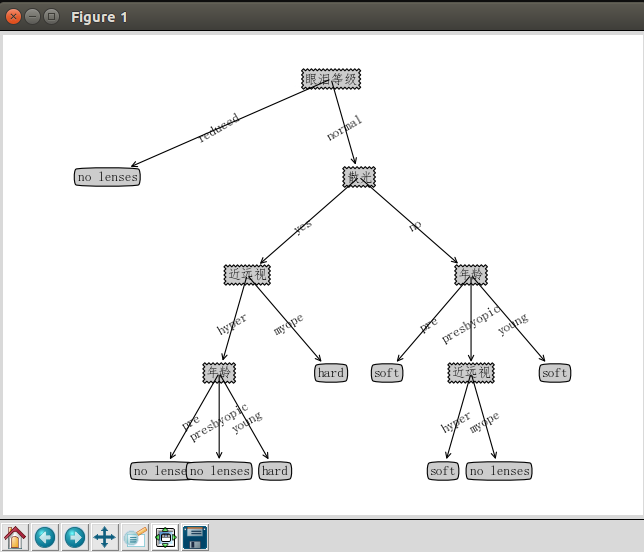
def plotNode(nodeTxt, centerPt, parentPt, nodeType):	#绘制带箭头的注解
    #annotate参数：nodeTxt：标注文本，xy：所要标注的位置坐标，xytext：标注文本所在位置，arrowprops：标注箭头属性信息
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
    
def plotMidText(cntrPt, parentPt, txtString):		#在父子节点间填充文本信息
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

def plotTree(myTree, parentPt, nodeTxt):		#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  			#计算宽与高
    depth = getTreeDepth(myTree)
    firstStr = myTree.keys()[0]     			#the text label for this node should be this
    print plotTree.xOff
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    print parentPt
    print cntrPt
    plotMidText(cntrPt, parentPt, nodeTxt)		#标记子节点属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD	#减少y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':	#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict

def createPlot(inTree):			#绘制树形图，调用了plotTree()
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))	#存储树的宽度
    plotTree.totalD = float(getTreeDepth(inTree))	#存储树的深度
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.show()

 

 

测试和存储分类器

1.测试算法：使用决策树执行分类

1
2
3
4
5
6
7
8
9
10
11
def classify(inputTree,featLabels,testVec):	#使用决策树的分类函数
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)	#将标签字符串转换为索引
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

 

1
2
3
4
5
6
7
8
9
10
11
12
myDat,labels = createDataSet()
Labels = labels
print "myDat="
print myDat
print "labels="
print labels

import treePlotter
myTree = treePlotter.retrieveTree(0)	#绘制树形图
print myTree
print classify(myTree,Labels,[0,1])

 

 2.使用算法：决策树的存储

1
2
3
4
5
6
7
8
9
10
11
def storeTree(inputTree,filename):	#使用pickle模块存储决策树
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()
    
def grabTree(filename):			#查看决策树
    import pickle
    fr = open(filename)
    return pickle.load(fr)

 

1
2
3
4
5
6
7
8
9
10
11
12
myDat,labels = createDataSet()
Labels = labels
print "myDat="
print myDat
print "labels="
print labels
import treePlotter
myTree = treePlotter.retrieveTree(0)	#绘制树形图
print myTree
storeTree(myTree,'classifierStorage.txt')
print grabTree('classifierStorage.txt')

 

示例：使用决策树预测隐形眼镜类型

 

1
2
3
4
5
6
7
8
9
10
11
12
import treePlotter
import simplejson
import ch
ch.set_ch()
from matplotlib import pyplot as plt
fr = open('lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]	#读取一行数据，以tab键分割并去掉空格
lensesLabels = [u'年龄',u'近远视',u'散光',u'眼泪等级']			#使用unicode，不然编码会报错
lensesTree = createTree(lenses,lensesLabels)
print simplejson.dumps(lensesTree, encoding="UTF-8", ensure_ascii=False)	#使用simplejson模块输出对象中的中文
treePlotter.createPlot(lensesTree)

 

tonglin0325

标签

标签云

AWS Airbnb Android CDH Doris ELK Flink Git Grafana HAProxy HBase Hadoop Hive Hudi InfluxDB JDBC JMeter JVM Java JavaWeb LaTex Linkedin Linux ML ML Infra MPP Maven MySQL Nexus OpenTSDB Paper Play Prometheus Python React Redis RocksDB Scala Solr Spark SpringBoot SpringMVC Thrift YARN antlr arthas avro cassandra clickhouse confluent docker filebeat flume golang google gradle hexo impala jenkins k8s kafka kerberos kudu ldap mac mongo mybatis nginx nlp open-falcon openwrt parquet presto ranger scyllaDB twitter zookeeper 刷题 前端 图存储及计算 多线程 广告系统 开发工具 数据结构 杂谈 正则表达式 算法 系统设计 计算机网络 设计模式

文章归档

最近文章