奇异值分解(Singular Value Decompositon,SVD),可以实现用小得多的数据集来表示原始数据集。
优点:简化数据,取出噪声,提高算法的结果
缺点:数据的转换可能难以理解
适用数据类型:数值型数据
SVD最早的应用之一是信息检索,我们称利用SVD的方法为隐形语义索引(LSI)或者隐形语义分析(LSA)。
在LSI中,一个矩阵是有文档和词语组成的。当我们在该矩阵上应用SVD的时候,就会构建出多个奇异值。这些奇异值代表了文档中的概念或者主题,这一特点可以用于更高效的文档检索。
SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间,然后再在该空间下计算其相似度。
SVD将原始的数据集矩阵Data分解成三个矩阵 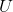 、
、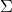 和
和 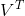 。
。
如果数据集矩阵Data是M×N的,那么 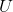 是M×M的、
是M×M的、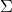 是M×N的、
是M×N的、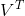 是N×N的。
是N×N的。
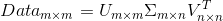
矩阵 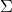 中只有从大到小排列的对角元素。在某个奇异值的数目(r个)之后,其他的奇异值都置为0,这就意味这数据集中仅有r个重要特征,而其余特征则都是噪声或者冗余特征。
中只有从大到小排列的对角元素。在某个奇异值的数目(r个)之后,其他的奇异值都置为0,这就意味这数据集中仅有r个重要特征,而其余特征则都是噪声或者冗余特征。
利用Python实现SVD
1 | >> X=[0.3619 0.2997 0.1331 0.3296;0.1695 0.3628 0.0817 0.2826;0.1159 0.5581 0.0828 0.3718;0.1508 0.1077 0.0539 0.1274] #Matlab |
1 | >> [U,S,V] = svd (X) #Matlab |
Python
1 | >>> from numpy import * |
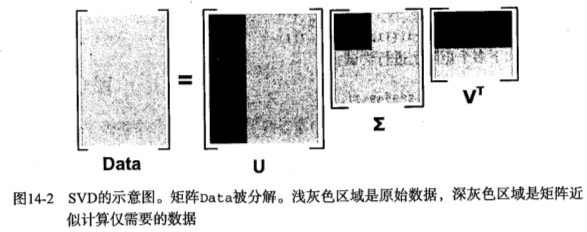
可以看到,在Sigma矩阵中8.12946379e-05 和 3.22769863e-05 值的量级太小了,所以可以忽略
所以Data矩阵的值就成了 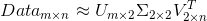
1 | >>> U,Sigma,VT = linalg.svd([[0.3619,0.2997,0.1331,0.3296],[0.1695,0.3628,0.0817,0.2826],[0.1159,0.5581,0.0828,0.3718],[0.1508,0.1077,0.0539,0.1274]]) |
1 | >>> import numpy as np |
经过SVD之后生成的三个矩阵相乘,得到的结果和原来的矩阵差不多
基于协同过滤(collaborative filtering)的推荐引擎
协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。这里的数据是从概念上组织成了类似矩阵的形式。当数据采用这种方式进行组织的时候,我们就可以比较用户或者物品之间的相似度。比如,如果电影和用户看过的电影之间的相似度很高,推荐算法就会认为用户喜欢这部电影。
相似度计算
第一种:使用欧式距离,相似度=1/(1+距离)
当距离为0的时候,相似度为1;当距离很大的时候,相似度趋近于0
第二种:皮尔逊相关系数
皮尔逊相关系数度量的是两个向量之间的相似度,相对于欧式距离的一个优势是,它对用户评级的量级并不敏感。
皮尔逊相关系数的取值范围在-1到+1之间,在NumPy中由**函数corrcoef()**计算
第三种:余弦相似度
余弦相似度计算的是两个向量夹角的余弦值,如果夹角为90度,则相似度为0;如果两个向量的方向相同,则相似度为1
** 余弦相似度的取值范围在-1到+1之间,在NumPy中由函数linalg.norm()**计算
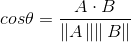
1 | from numpy import * |
1 | # coding:utf-8 |
1 | 0.129731907557 |
